Arguments en faveur de l'amélioration continue

2019-10-15 - Écrit par Jayson McIntosh, en collaboration avec l'équipe de Stratégie TI

Dernière modification: 2019-11-19

Dans le livre “The DevOps Handbook”, les auteurs démontrent que les équipes devraient consacrer au moins 20 % de leur temps à la réduction de la dette technique.

Note : Traduction non-officielle de l’anglais ci-dessous :

L’accord [entre les propriétaires de produits et] l’ingénierie se déroule comme suit : La gestion des produits prend 20 % de la capacité de l’équipe dès le départ et la donne à l’ingénierie pour qu’elle la dépense comme bon lui semble.

Ils pourrons l’utiliser pour réécrire, réarchitecter ou refactoriser des parties problématiques du code… tout ce qu’ils croient nécessaire pour éviter d’avoir à venir dire un jour à l’équipe : “ Nous devons arrêter et réécrire [tout notre code] “. Si vous êtes en très mauvaise posture aujourd’hui, vous pourriez avoir besoin de 30 % de ces ressources ou même plus. Cependant, je deviens nerveux quand je trouve des équipes qui pensent qu’elles peuvent s’en sortir avec beaucoup moins que 20 %.

Je vais résumer cela en suggérant que toutes les équipes devraient consacrer au moins 20 % de leur temps à améliorer leur façon de travailler. Dans le cas de l’équipe avec laquelle je travaille, nous rédigeons des documents et réalisons des preuves de concept pour démontrer l’efficacité des idées que nous proposons. Un jour après le travail, je discutais de la modélisation de notre équipe en tant qu’équipe facilitatrice, tirée de “Team Topologies”, avec un collègue. Dans le livre, ils recommandent qu’une équipe facilitatrice passe du temps à aider d’autres équipes à intégrer de nouvelles technologies ou trouver de meilleures façons de travailler. Mon collègue m’a mis au défi sur notre capacité à nous vendre en tant qu’équipe d’apprentissage. Les gens sont occupés, pourquoi voudraient-ils se ralentir en consacrant du temps loin de leurs priorités pour s’améliorer? Comment vendriez-vous cela à une équipe qui travaille déjà à 120 % de sa capacité?

Bon nombre d’entre nous connaissent déjà, grâce au “Phoenix Project”, la justification anecdotique de l’engagement de consacrer du temps à l’amélioration de notre processus. Si une personne s’est vraiment passionnée pour le “Phoenix Project”, elle peut investir du temps pour en apprendre davantage sur la magie de DevOps dans des livres comme The DevOps Handbook (ce que je vous suggère de faire). Cependant, si vous êtes dans une position où vous avez besoin de faire rapidement une analyse de rentabilisation de l’amélioration continue, comment s’y prendre? C’est ce que je vais essayer de faire ici. Présenter un argument succinct en utilisant des mathématiques simples pour démontrer la valeur de l’amélioration continue.

Trop long; pas lu (TLDR)

Le “trop long; pas lu” de cet article est que “continue”, en termes plus formels, signifie la capitalisation. Ou, selon votre jargon préféré, exponentiel. Si vous tracez le graphique de sortie avec l’axe Y comme “unités produites” et X comme temps, alors l’équipe qui s’améliore continuellement augmentera son rendement de façon exponentielle. Et étant donné une valeur arbitrairement grande n (ou lorsque n approche l’infini) alors exponentielle battra toujours linéaire. Étant donné que nos équipes existent pour une période arbitrairement longue (n), les équipes qui s’améliorent continuellement seront plus productives qu’une équipe qui ne le fait pas.

Si ça sonnait un peu mathématique ou jargon, on va l’expliquer plus en détail ci-dessous.

Arguments en faveur de l’amélioration continue

Cette démonstration a été réalisée en utilisant le site fantastique, desmos.

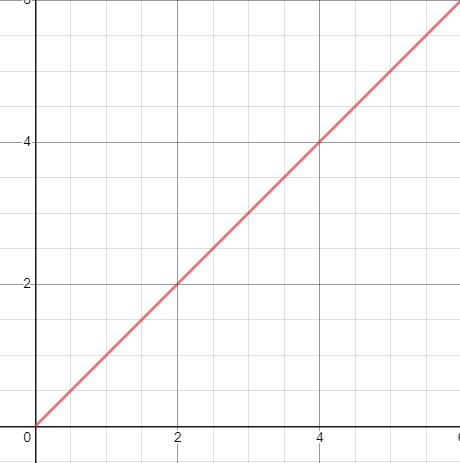
Si nous traçons f(x) = x nous obtiendrons une ligne comme suit

Cette image est celle d'un graphique linéaire. Elle a un axe x allant de 0 à 6 et un axe y allant de 0 à 6. Il y a une ligne droite rouge sur le graphique qui commence au point 0,0 et va jusqu'au point x=6, y=6

Nous définissons l’axe des y (l’axe vertical) comme étant l’unité totale de la valeur d’affaires produite, et l’axe des x comme étant l’axe du temps. La ligne représente alors le total des unités de la valeur d’affaires produites sur une certaine unité de temps.
Pour les besoins de cet exemple, disons que chaque augmentation de x est d’un mois.

Cette ligne suppose que, semaine après semaine, l’équipe continue à faire son travail “comme d’habitude”, ou la fameuse approche “nous l’avons toujours fait comme ça”. Avec cette approche, l’équipe produira (en moyenne) les mêmes unités de valeur d’affaires chaque semaine. Si vous travaillez plus de 100 % cette semaine, vous le serez aussi la semaine prochaine.

Quelle est l’alternative? L’amélioration continue.

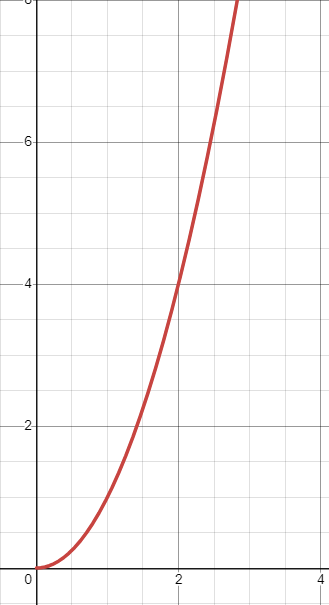
Si nous continuons à améliorer nos processus et nos outils semaine après semaine, nous nous améliorerons continuellement, ce qui nous permettra de produire plus de valeur d’affaires sur une période donnée. Ceci devrait nous donner une courbe exponentielle, qui ressemble à ceci

f(x) = x²

Cette image est un graphique linéaire représentant la fonction f(x) = x^2.
Il a un axe X allant de 0 à 4 et un axe Y allant de 0 à 8.
Il y a une ligne rouge courbe sur le graphique qui commence à (0,0) et monte exponentiellement jusqu'à (2,83, 8)

La chose la plus évidente que nous remarquons est que la fonction exponentielle croît beaucoup plus vite. On peut toutefois exposer le fait qu’il y a une perte initiale de productivité si l’on passe du temps à s’améliorer plutôt qu’à faire son travail, alors nous devons le prendre en compte. Pour ce faire, nous devons soustraire une valeur de f(x) pour tenir compte de la perte de productivité. Pour chaque incrément dans le temps, alors, nous perdrons un certain pourcentage de notre temps. Où x représente le temps, ceci peut être écrit comme suit

x * [un certain pourcentage de perte de productivité]

Ou, pour être plus succinct, nous pouvons remplacer [un certain pourcentage de perte de productivité] par l. Alors nous aurons

x * l, où l est le temps passé par jour à s’améliorer.

Avec cet ajout, nous avons

f(x) = x² - (x*l)

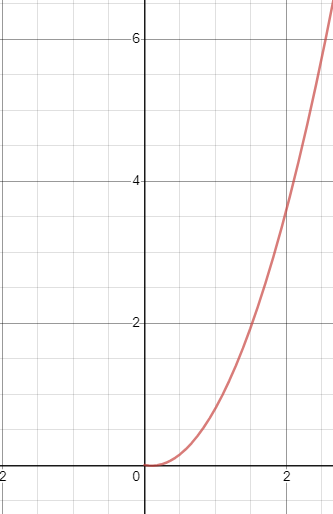
Que se passe-t-il lorsque nous traçons ce graphique? Supposons que nous avons consacré 20 % de notre journée à l’amélioration continue. Et qu’Ensuite, nous perdons 20 % de notre productivité par mois.

Cette image est un graphique linéaire représentant la fonction f(x) = x2 - (x*l) avec un axe X allant de -2 à 2 et un axe Y allant de 0 à 6.25.
Il y a une ligne rouge courbe sur le graphique qui commence à (0,0) et augmente exponentiellement jusqu'à environ (2.25, 6.25)

Remarquez en bas que la courbe s’aplatit légèrement. Cette baisse de productivité est toujours présente puisque x (le temps) augmente. Cependant, un exposant battra toujours une progression linéaire (anglais). La prochaine étape évidente serait alors de tracer un graphique de notre façon de travailler “telle quelle” par rapport à notre méthode d’amélioration continue, et de voir combien de temps il faudrait pour qu’une équipe en amélioration continue soit plus productive que l’équipe qui continue à travailler de la même façon, jour après jour. Auparavant, cependant, dans notre calcul précédent, nous utilisions x^2, qui est une courbe qui croît très rapidement, et jusqu’à présent, nous n’avons pas justifié notre choix de la valeur arbitraire de 2. Une autre façon d’écrire cela aurait pu être

x² = x¹⁺¹

Lorsque nous parlons de points de pourcentage, nous calculons à l’aide de points décimaux. Par conséquent, 1 = 1,0 = 100 %. Par conséquent, comme nous l’avons écrit précédemment, nous affirmons que notre productivité augmente de 100 % par jour! Si quelqu’un a trouvé un moyen de le faire, nous aimerions avoir de vos nouvelles! Malheureusement, si vous vivez dans le royaume des simples mortels comme moi, une augmentation de 100 % de la productivité par jour est probablement impossible à atteindre.

Nous pouvons réécrire notre fonction d’augmentation de la productivité comme suit

f(x) = x^{1+[le volume d’augmentation de productivité que nous prévoyons par mois consacré à l’amélioration continue]}

C’est très long à dire, donc si nous fixons [le volume d’augmentation de productivité que nous prévoyons par mois consacré à l’amélioration continue] = r, alors nous avons

x² = x^1+r

Où r est un certain pourcentage d’augmentation de la productivité.

D’accord. On y est presque! Notre fonction de cartographie de la productivité d’une équipe en amélioration continue est la suivante

f(x) = x^1+r - (x*l)

Où r est égal au taux d’amélioration
Et l est égal au volume de temps consacré à l’amélioration continue

Ensuite, nous allons choisir quelques valeurs qui font du sens. Comme nous l’avons mentionné, dans le “DevOps Handbook”, ils recommandent de consacrer 20 % de votre temps à la réduction de la dette technique ou à l’amélioration des processus. Donc, pour l, nous choisirons 20 %, soit 0,2

Maintenant, combien d’amélioration attendons-nous de 20 % de notre temps consacré à l’amélioration? En tant qu’employé du gouvernement, je sais que dans certains cas, ce retour peut être gargantuesque. Par exemple, l’Estonie affirme économiser 820 années de temps de travail annuellement grâce à l’utilisation de services numériques automatisés (anglais). Pour notre exemple, cependant, comme nous le verrons, le taux d’amélioration n’est pas très important. Vous finirez toujours par devenir plus productif si vous vous améliorez continuellement pendant assez longtemps. D’accord, alors, choisissons 10 %, ce qui équivaut à 0,1. Nous supposons donc que pour un investissement de temps de 20 %, vous en gagnerez au moins la moitié en efficacité. Conservateur, au mieux. Notre fonction devient alors

f(x) = x^1+0.1 - (x*.2)

f(x) = x^1.1 - (x*.2)

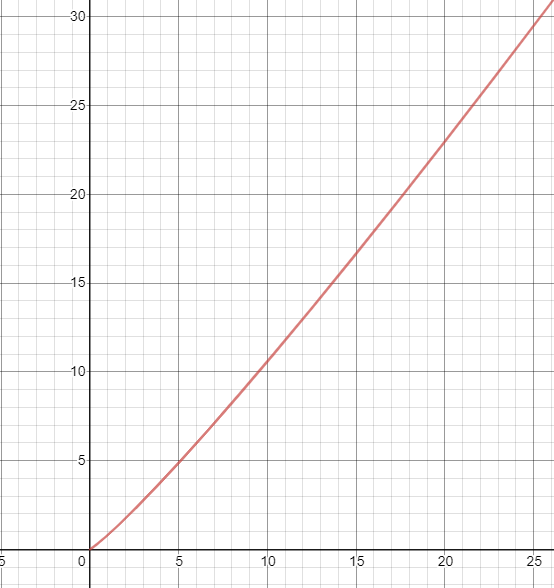
Et si nous traçons ce graphique, nous obtenons la courbe suivante

Cette image est un graphique linéaire représentant la fonction f(x) = x^(1.1) - (x*.2) avec un axe X allant de -5 à 25 et un axe Y allant de 0 à 30.
Il y a une ligne rouge droite sur le graphique qui commence à (0,0) et augmente exponentiellement jusqu'à environ (25, 29.5). Deux lignes se croisent sur le (5.2, 5.2)

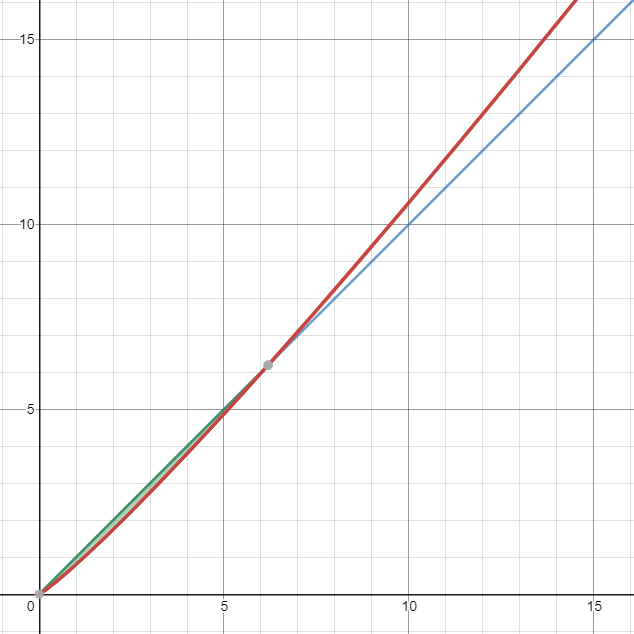
Super! Quelle est la prochaine étape? Disons que nous comparons cela à une équipe qui ne s’améliore pas continuellement et qui continue de faire les choses au jour le jour, “comme elle les a toujours faites”.

Cette image est un graphique linéaire représentant la fonction f(x) = x^(1.1) - (x*.2) par rapport à la fonction f(x) = x.
Il y a un axe X allant de 0 à 15 et un axe Y allant de 0 à 15.
Il y a une ligne rouge sur le graphique qui commence à (0,0) et monte exponentiellement jusqu'à environ (14, 16).
Il y a une ligne bleue sur le graphique qui commence à (0,0) et va directement à (15,15)

Nous pouvons voir que la ligne rouge, qui représente l’équipe qui s’améliore continuellement pendant 20 % de sa journée pour un petit rendement de 10 % de productivité, sera plus productive dans environ 6 mois (ou 6,192 mois, pour être exact). Même si vous réduisez de moitié les gains de productivité (à 5 %, ou 0,05), vous constaterez quand même qu’avant 39 mois, l’équipe qui s’améliore continuellement finira inévitablement par dépasser l’équipe qui ne le fait pas.

Nous avons démontré que même si le compromis entre le temps investi et le gain potentiel est faible, si l’on améliore continuellement son équipe, avec le temps, elle deviendra plus productive que l’équipe qui ne le fait pas.

Imaginez si elle avait commencé à s’améliorer continuellement il y a plusieurs années, pensez à la productivité qu’elle aurait maintenant! Ne faites pas la même erreur que nos prédécesseurs. Commencez à vous améliorer sans cesse dès maintenant! Vos futurs membres d’équipe, vos futurs patrons et votre futur vous-même vous remercieront.

Pour satisfaire le but de cet article, on peut s’arrêter ici. Si vous souhaitez jouer avec quelques nombres présentés dans ce billet avec desmos, cliquez ici. Si vous êtes intéressés par de plus amples détails, ci-dessous, nous allons parler de la façon de décider du compromis optimal entre les gains de productivité et le temps investi.

La fin

Merci de m’avoir écouté! C’était ma tentative de passer d’une démarche simple à une plus complexe pour tenter de définir plus formellement et rigoureusement la logique qui supporte l’engagement d’amélioration continue. Dans la première partie de ce document Arguments en faveur de l’amélioration continue, j’espérais fournir une présentation succincte et facile à utiliser pour que les gens commencent à s’améliorer continuellement sans avoir à lire tous les livres… bien qu’il serait préférable qu’ils le fassent. Il suffit de se rappeler un peu de nos vieux livres de maths. Le prochain billet s’adressera aux lecteurs plus engagés qui souhaitent explorer plus en profondeur les résultats souhaités de l’amélioration continue et ce que nous devrions prendre en considération à cet effet. Ce billet de blogue a été un plaisir à écrire.

Merci de votre lecture!

Mis à jour le 2019-11-19: L’auteur principal de l’article a été ajouté.

Mis à jour le 2019-11-13: La section Plongée plus profonde a été déplacée vers un futur article pour raccourcir la longueur de celui-ci et la conclusion a été adaptée pour mieux représenter cette nouvelle structure.